算法导论

一、算法基础

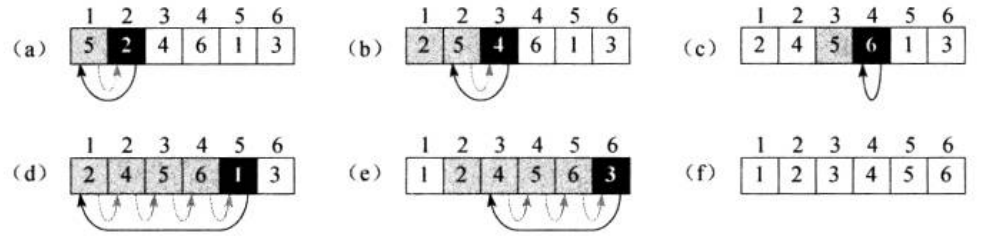
插入排序

    /**
     * 插入排序：类似于抓扑克牌，从牌堆中拿牌，跟手上已经排序的排作比较，插入合适的位置
     * 时间复杂度O（n）-O（n2）
     * @param data
     * @return
     */
    public static int[] insertSort(int[] data){
        /*
         * 从第二个元素开始遍历，通过变量持有，从后往前比较，将元素往后移，如果小于则继续往前，直至最后，将持有元素插入。
         */
        for (int i=1;i<data.length;i++){
            int a=data[i];
            int j=i-1;
            while (j>=0 && a<data[j]){
                data[j+1]=data[j];
                j--;
            }
            data[j+1]=a;
        }
        return data;
    }

二、分治算法

将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时有三个步骤：

分解原问题为若干子问题，这些子问题是原问题的规模较小的实例；

解决这些子问题，递归地求解各个子问题。然后，若子问题地规模足够小，则直接求解；

合并这些子问题的解成原问题的解；

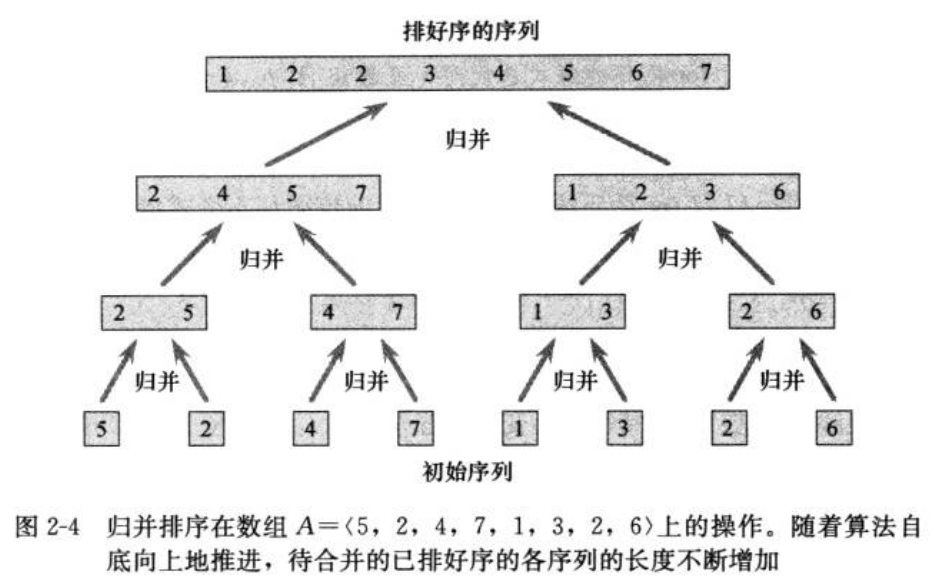
2.1归并排序

    /**
     * 分治排序：
     *      整体思想，将大问题，切割成小问题，解决小问题然后将结果进行归并
     *      两个有序的牌堆，将他们进行合并，只需要比较第一张大小，谁小就拿谁，然后重新翻开一张重新比较；
     *      问题关键，怎么得到两个有序的牌堆，将数组，对半分分分，一直切分到只有1个数的时候，然后进行归并；
     * 时间复杂度：O（nlgn）
     * @param data 数组
     * @param s 左起点
     * @param e 右起点
     */
    public static void dacSort(int[] data,int s,int e){
        if (s<e){
            int m=(s+e)/2;
            dacSort(data,s,m);
            dacSort(data,m+1,e);
            merge(data,s,m,e);
        }
    }
    private static void merge(int[] data,int p ,int q,int r){
        int[] temp = new int[r - p + 1];
        int x=p,y=q+1;
        int i=0;
        while (x<=q && y<=r){
            if (data[x]<data[y]){
                temp[i]=data[x];
                x++;
            }else {
                temp[i]=data[y];
                y++;
            }
            i++;
        }
        while (x<=q){
            temp[i++]=data[x++];
        }
        while (y<=r){
            temp[i++]=data[y++];
        }
        for (int n=0;n<temp.length;n++){
            data[n+p]=temp[n];
        }
    }

2.2最大子数组问题

/**
     * 最大子数组问题：求得数组连续子序列的最大和
     *      将数组一分为二，最大子数组有三种情况：一包含在左子数组中，二包含在右子数组中，三被一分为二；
     *      第三种情况：只需分别从中间向左，以及从中间向右，求得两个最大值的和，即为结果；
     *      而第一、第二种情况，则是将最大子数组问题，分割为两个相同但规模变小的问题，可递归直至一个元素时，直接返回；
     * @param data 数组
     * @param s 左起点
     * @param e 右起点
     * @return
     */
    public static int findMax(int[] data,int s,int e){
        if (s==e){
            return data[s];
        }
        int mid=(s+e)/2;
        int a = findMax(data, s, mid);
        int b = findMax(data, mid+1, e);
        int c=findMaxByMid(data,s,e,mid);
        int max = Math.max(Math.max(a, b), c);
        return max;
    }
    private static int findMaxByMid(int[] data,int s,int e,int mid){
        int result1=0;
        int sum1=0;
        for (int i=mid;i>=s;i--){
            sum1+=data[i];
            if (result1<sum1){
                result1=sum1;
            }
        }
        int result2=0;
        int sum2=0;
        for (int i=mid+1;i<e;i++){
            sum2+=data[i];
            if (result2<sum2){
                result2=sum2;
            }
        }
        return result1+result2;
    }

三、堆排序

堆排序的时间复杂度是O(nlgn)，具有空间原址性。

/**
 * Java堆实现
 *      属性：数组实现的堆，堆的长度(堆长度小于等于数组长度)
 *      方法：①创建堆，②维护堆的性值
 */
class Heap{
    public Heap(){}
    private int[] data;
    private int heapSize;

    public int[] getData() {
        return data;
    }

    public void setData(int[] data) {
        this.data = data;
    }

    public int getHeapSize() {
        return heapSize;
    }

    public void setHeapSize(int heapSize) {
        this.heapSize = heapSize;
    }

    /**
     * 创建堆：
     *      堆操作都是原址操作，直接赋值数组和长度
     *      堆是完全二叉树，除了最底层，叶子节点都是铺满的，特性：堆的二分之一都是叶子节点
     *      叶子节点是不需要维护堆特性的，子节点从后往前去维护堆特性，最后得到最大堆
     *      时间复杂度：O(nlgn)
     * @param data 数据
     */
    public void buildMaxHeap(int[] data){
        this.data=data;
        this.heapSize=data.length;
        for (int i=data.length/2;i>=1;i--){
            maxHeapify(data,i);
        }
    }

    /**
     * 维护堆特性：
     *      最后的堆数据，其实就是二叉树的层序遍历，特性是：当前节点的左孩子和右孩子分别是i*2和i*2+1
     *      与孩子节点比较大小，如果小则交换，并且需要递归去维护交换后的节点的特性，如果大，则不需要其他操作
     *      添加边界比较，保证能够及时退出
     * @param data
     * @param i
     */
    public void maxHeapify(int[] data, int i) {
        int left=i*2;
        int right=i*2+1;
        int max=i;
        if (left<=heapSize && data[left-1]>data[i-1]){
            max=left;
        }
        if (right<=heapSize && data[max-1]<data[right-1]){
            max=right;
        }
        int temp=data[max-1];
        data[max-1]=data[i-1];
        data[i-1]=temp;
        if (max!=i){
            maxHeapify(data,max);
        }
    }
}

有了Java的堆实现，想要进行推排序就简单很多

public class HeapSort {
    /*
     * 构建最大堆;
     * 交换第一个和最后一个数;
     * 将堆的长度减一;
     * 维护最大堆的特性，重复以上操作;
     * @param data
     */
    public static void heapSort(int[] data){
        Heap heap = new Heap();
        heap.buildMaxHeap(data);
        for (int i=data.length-1;i>=1;i--){
            int temp=data[i];
            data[i]=data[0];
            data[0]=temp;
            heap.setHeapSize(heap.getHeapSize()-1);
            heap.maxHeapify(data,1);

        }
    }
}

四、快速排序

    /**
     * 快速排序：原址排序，取最后一个数字，与之进行比较，大的放右边，小的放左边，数组就被划分为两部分，递归分别对这两部分数组操作；
     *          ①比较，类似于双指针，i，j两个指针一个标记小于的边界，一个用来遍历数组，j指针遍历分别于数字进行比较，如果小于数字，
     *          则将i指针右移一位，并交换i和j的值；如果大于，继续遍历；i只有当j遍历小于后才会+1，但是因为i和j之间有大于的数，所以
     *          将当前小于的数于大于的数交换，保证i边界；
     *          ②j遍历结束后，交换i后一位大于的数字，即i+1前小于，i+1后小于
     *          时间复杂度：O(nlgn)-O(n2)
     * @param data
     */
    public static void quickSort(int[] data,int start,int end){
        if (start>=end){
            return ;
        }
        int mid=partition(data,start,end);
        quickSort(data,start,mid-1);
        quickSort(data,mid+1,end);

    }

    private static int partition(int[] data, int start, int end) {
        int num=data[end];
        int temp=start-1;
        for (int i=start;i<end;i++){
            if (num>=data[i]){
                temp++;
                int a=data[i];
                data[i]=data[temp];
                data[temp]=a;
            }
        }
        temp++;
        data[end]=data[temp];
        data[temp]=num;
        return temp;
    }

五、计数排序

    /**
     * 计数排序：
     *      根据原数组的值的范围，确定一个临时数组。遍历原数组，在临时数组的该值位置上+1，遍历临时数据，累加；
     *      遍历原数组，找到该值对应的临时数组的值，该值即为排序数组中的位置，并将临时数组-1（为了处理数相同的情况）
     *      不同于比较排序，通过值来确定位置来间接获得大小,其实就是通过空间换时间，不适合值范围太大的数组
     *      时间复杂度：O（n）
     * @param data 原数组
     * @param result 结果数组
     * @param k 值的范围（最大值）
     */
    public static void countingSort(int[] data,int[] result,int k){
        int[] temp = new int[k + 1];
        for (int num : data) {
            temp[num]+=1;
        }
        for (int i=1;i<temp.length;i++){
            temp[i]+=temp[i-1];
        }
        for (int i=0;i<result.length;i++){
            result[temp[data[i]]-1]=data[i];
            temp[data[i]]-=1;
        }
    }